Lecture 22

这一节是上一节的延续，还是关于合作。

本节最关键的公式：

gain if cheat today $\le$ [value of relation after cooperation] - [value of relation after cheating]

右边的式子第一项表示的是promise，第二项表示的是threat。

扳机策略（grim trigger）

有下面的囚徒困境博弈：

扣扳机策略：

如果前面一直合作，那么一直合作；一旦对方叛变，以后都不合作。

为了让双方有合作共赢的动机，假设每轮有$\delta$的概率进行下一轮的博弈（实际上还有不同的方式来激励下一轮的博弈）：

$3-2 \le ((2+2*\delta+2*\delta^2+\dots)-0)\delta$

假设博弈无数轮：

$3-2 \le ((\frac{2}{1-\delta})-0)\delta$

最后得到$\delta范围为\delta \ge \frac{1}{3}$

lesson:

1. 如果使用扳机策略（背叛的代价），并且继续合作的概率大于$\frac{1}{3}$（合作的动机），我们能够在囚徒困境中达到合作的关系。
2. 为了未来提供合作，必须提供充足的动机。

一回合惩罚机制

如果之前一直合作，那么就一直合作；一旦产生叛变，下一回就叛变，经过一个回合后继续合作，相当于增加一个回合的惩罚。

那么上面的公式为

$3-2 \le ((\frac{2}{1-\delta})-\delta*\frac{2}{1-\delta})\delta$

求解出来$\delta \ge \frac{1}{2}$

lesson:

如果惩罚的力度越小，那么未来合作的概率应该越大。反过来说，如果未来的合作机会不明朗，那么就增加惩罚力度。

市场聘用

一个跨国公司决定在某地进行投资和雇佣，如果进行投资，那么应该给工人多少的薪水？

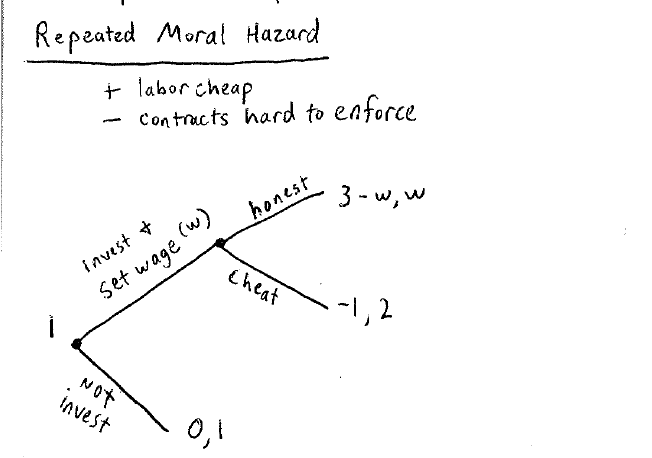
投资的分额假设是1

如果不进行投资，那么跨国公司不赚钱，工人当地的薪水为1；

若进行投资，如果工人携款潜逃了，那么收益矩阵为(-1, 2);

如果双方进行合作，那么收益是(3-w, w)。

考虑到下一次合作的概率为$\delta$。

那么得到公式：$2-w \le (\frac{w}{1-\delta}-\frac{1}{1-\delta})\delta$

解的$w \ge 2-\delta$

如果$\delta = 0$，那么只有一次合作，那么工人一定携款潜逃。

如果$\delta = 1$，那么这个跨国公司就相当于是本地开的，w = 1。